How to Draw Sonic the Hedgehog : Step by Step Drawing Lesson

114 Comments

« GO TO PREVIOUS PAGE» GO TO NEXT PAGE

Page : 1 2 3

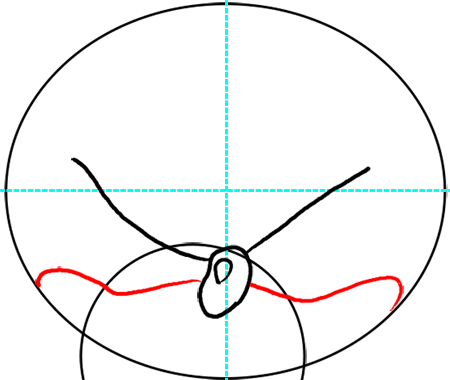
Step 7

Now draw 2 squiggled lines from the middle of the nose to the outside of the circle.

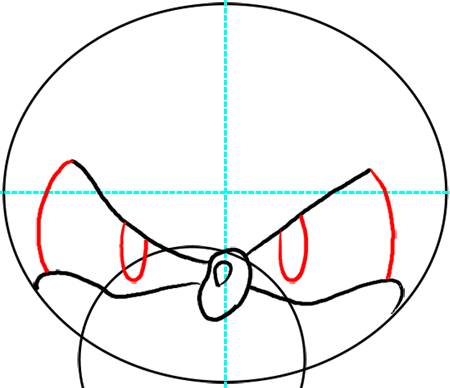
Step 8

Now draw a curved line for the outside of the eyes. Also draw a letter ‘U’ for each of Sonic’s irises / pupils.

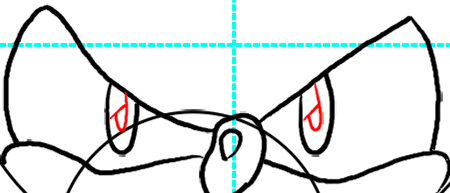
Step 9

Now to make the highlight in the eye draw a slanted line downards from the middle of the letter ‘U’ that you just drew (making it look like a letter ‘J’ with a square in it.

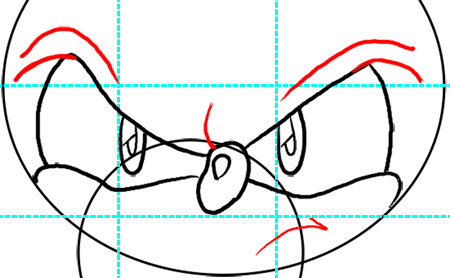
Step 10

Now draw Sonic’s furrowed brow by drawing 2 downward curved lines above his eyes. I drew blue lines along the left edge of each eye to show you that the brow lines start at about the same vertical position. Also draw a curved line above his nose. To draw his mouth draw a backwards checkmark.

Step 11

Now draw Sonic the Hedgehog’s ears. I drew a line along the right side of his mouth to show you that the right ear starts at about the same point that the mouth does. Also notice that I drew a horizontal line along the top of the left brow and this is where the right ear ends.

Step 12

Now to draw Sonic’s hair. To get the right proportions I wanted you to nitice that the top of the hair to the top of his head is the same as the top of the head to the bottom of his nose.

Step 13

Now draw Sonic’s arms as 2 sideways number ’11’s.

« GO TO PREVIOUS PAGE» GO TO NEXT PAGE

Page : 1 2 3

Pages: 1 2 3

114 Comments

  9. john

    ahhhhhhhhhhhhhhhhhhhhh I LOVE HIM !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! YAH

    Reply

  22. henry

    OMg!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! i looooooooooooooooooooooooooooooooooooooooooooooooooooooovvvvvvvvvvvvvvvvvvvvvvvvveeeeeeeeeeeeeeeeeeeeeeeeeeee sonic i love this tutorial thx

    Reply

  23. Tania_Da_FairyPrincess

    When I was a little girl I was very very addicted to sonic I had alot of the games like sonic & the black night,but mostly sonic heroes I was supporting Sonamy (sonicXamy) and all that I love their music,but the biggest problem is that I never knew how to draw them (/.\) but thanks to you Ive learned and I feel like a true sonic fan thank you <3

    Reply

  28. coollllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll and super coollllllllllllllllllllllllllllllllllllllllllllllllll !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

    Reply

  38. Shelynni

    omg drawing sonic was one BIIIIIG adventure for me! this was epic!!!!!!!!!!!!!!!! i think i did good for once….. XD

    Reply

  42. ???

    my mum loves sonic the hedgehog so i had a g at drawing him and he turned out really well t6hanks so much to the person who made this site it has made my mums dad!!! 🙂 🙂

    Reply

  44. Dávid

    I live in Australia, and I have to say; I love your drawing! It was very detailed. A very splendid well done from me! 😉

    Reply

  60. Sharp-e 147

    hey im an 11 year old girl with a real talent for drawing as far as every one has told me and i love sonic the hedghog i tried drawing it today and it turned out amazingley well if i can draw it i am shaw anyone can 🙂 😛 😀 ;D

    Reply

    • admin

      Just keep trying and you will get better each time. It might help you to trace it by taping it on the window and placing another piece of paper on top of – the sun will shine through the paper and allow you to trace it. Tracing is a good way to learn – just keep trying. Good luck. 🙂

      Reply

  66. Blake

    good drawing, i will definatly recomend this site to my 8 yearold cousin and 7 and 10 yearold neibors ( they luv sonic. make 1 of sonic unleashed and i will be amazed by the progress of the site

    Reply

  69. Nunyabidness ppl

    my friend is an awesome drawer, i bet he could do it better than everyone here with some modifications. he’s 11 and he DEFINITELY could do it. 😉

    Reply

  70. Nunyabidness ppl

    i guess i just cant draw because no matter wut i do i just cant draw him right. oh well, a fan can still be a fan even if they cant draw i guess. lol. 😉

    Reply

  86. mine looks REALLY crap-y because i used a pen and just kinda doodled him out. but your able to tell what character he is so he’s not too bad!! i wish they had a “how to draw shadow”. cuz he’s my fav out of all the sonic characters. actually, he’s my all-time fav. oh and how old do i have to be to be on here? cuz i’m 11.

    Reply

  99. Birdie

    Thanks for posting. My daughter (11) just followed your tutorial and it turned out fantastic – you’d be proud!

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *